How to think like a computer¶
These days computers can perform complex task. However, at their core computers only have a relatively small set of basic capabilities. Information is stored as zeros and ones and Boolean logic is used to perform calculations.
This chapter will cover fundamental aspects of computing required to learn scripting and programming. It will introduce bits and bytes and how they can be used to represent numbers and characters (as in letters and symbols). The chapter will also give a brief overview of how a computer stores information and performs calculations.
Binary, bits and bytes¶
In computing a bit is the smallest unit of information and it can be either zero or one. Suppose that we wanted to represent a positive integer using zeros and ones. We can achieve this using using the base-2 numeral systems, a.k.a. binary.
Take for example the number 108. This number can be represented as two sets of hundreds and eight sets of ones (as well as zero sets of tens).
The equations above illustrate the basis of the base-10 numeral system. Note that the base of the exponent in each term is ten. This means that one needs ten states to represent numbers. However, computers only have two states 0 and 1. To express an integer in binary we therefore need to formulate it so that the base of each exponent is 2.
So to express 108 as binary we could use the bits 1101100.
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
In computing bits are often grouped together and the most common grouping is to bundle 8-bits together, this is known as a byte. One byte can therefore have 256 unique states. An unsigned 8-bit integer, stored in a byte, can therefore represent any integer ranging from 0 to 255.
To recap, in computing a bit is the smallest unit of information and it can be either zero or one, and a byte is eight bits grouped together. Using several bits we can express integers using the binary numeral system.
Character encodings¶
If a computer only works in terms of zeros and ones how can one use it to read and write text? This is the subject of character encodings.
One of the most prevalent character encodings is ASCII (American Standard Code for Information Interchange), which was first published in 1963. It has its roots in telegraphic codes. Based on the English alphabet it encodes 128 characters into 7-bit integers (Fig. 1). These characters include: 0-9, a-z, A-Z, the space character, punctuation symbols and control codes for operating Teletype machines.
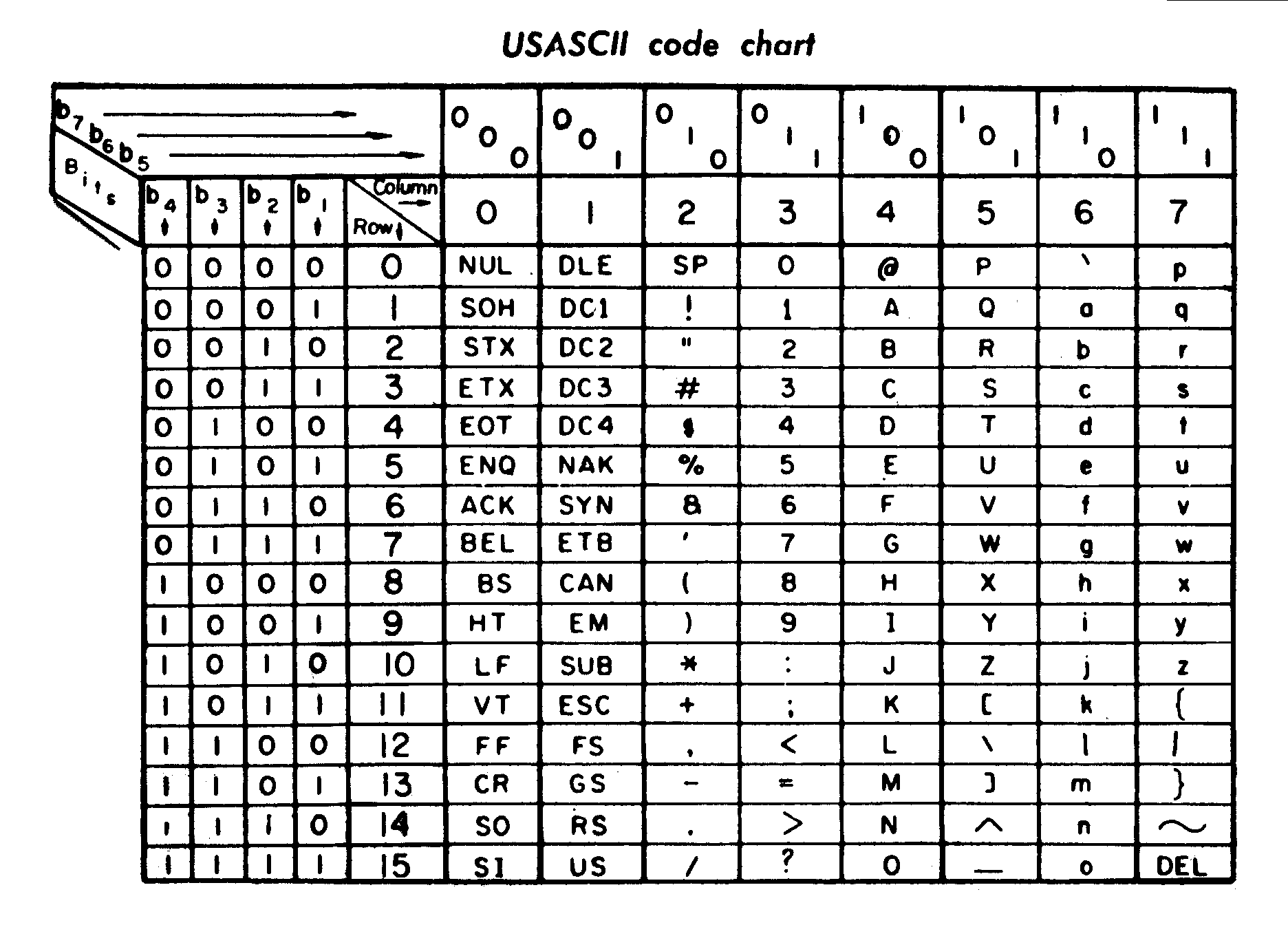
Fig. 1 ASCII Code Chart, scanner copied from the material delivered with TermiNet 300 impact type printer with Keyboard, February 1972, General Electric Data communication Product Dept., Waynesboro VA. By Namazu-tron [Public domain], via Wikimedia Commons.
Although many of the control characters are now obsolete some of them still form the basis of how we interpret text in computers. For example the “line feed” character, which originally moved the paper in the printer forward, is now used to represent new lines in text documents.
In going from Teletype machines to computers different operating systems had different interpretations on how new lines should be represented. One surviving convention, still in use in Windows, requires both the “line feed” and the “carriage return” characters. The former representing the advancement of paper in the printer and the latter the repositioning of the print-head. Another convention, used in Unix-like systems, is to simply use the line feed character to represent new lines. This can result in compatibility issues when opening Unix-like text files in some Windows programs. For example when one opens a multi-line file with Unix-based line endings in Notepad the text appears like one long line.
Many other character encodings are based on ASCII. A famous example is ISO-8859-1 (Latin 1), which uses an eighth bit to expand the ASCII character set to include the remaining characters from the Latin script.
These days the emergent standard is Unicode, which provides a standard encoding for dealing with most of the worlds writing systems. Unicode is backwards compatible with ASCII and ISO-8859-1 in that Unicode’s code points, the natural numbers used to assign unique characters, have the same values as those of the ASCII and ISO-8859-1 encodings.
So in computers “text” is really just a convention that maps integers to characters, or more formally a character encoding.
Real numbers¶
So we have learnt that integers can be represented in computers with zeros and ones by making use of the binary numeral system. Let us now discuss how real numbers can be represented and some issues that one can come across when working with these.
One way of storing and working with real numbers is to use the fixed-point number representation. A fixed-point number is basically an integer that is scaled by an implicit factor. So if the implicit scaling factor was \(1/10\) and the explicit integer was \(127\) then the real number represented would be \(12.7\).
The fixed-point number representation has the disadvantage that the range of numbers that can be represented is relatively small. Consider an unsigned 8-bit integer. It can represent the range \(0\) to \(255\). With an implicit scaling factor of \(1/10\) it can represent the numbers \(0.0\) to \(25.5\) with a step size of \(0.1\). With an implicit scaling factor of \(1/100\) it could represent the numbers \(0.00\) to \(2.55\) with a step size of \(0.01\).
The floating-point number was invented to work around the inherent small range limitation of fixed-point number representations. Floating-point numbers basically allow the decimal (radix) point to float. This means that numbers of differing orders of magnitude can be expressed using the same units. It is similar to scientific notation where the distance to the moon can be expressed as \(3.844 * 10^8\) and the size of a typical bacterium can be expressed as \(1.0 * 10^{-6}\). A consequence of this is that the numbers that can be expressed are not uniformly spaced, i.e. as the size of the exponent increases the step size between two representable numbers increases.
Not all numbers can be represented precisely using floating-point numbers. Furthermore, arithmetic operations on floating-point numbers cannot truly represent arithmetic operations. This can lead to issues with accuracy. We can illustrate this using Python (we will get more details on scripting and Python in the Data analysis chapter).
>>> 0.6 / 0.2
2.9999999999999996
In the above a rounding error of \(4 * 10^{-16}\) has been introduced as a consequence of working with floating point representations of numbers.
Boolean logic¶
Boolean logic is a mathematical formalism for describing logical relations.
In Boolean logic things are either True or False. These truth values
are often represented as 1 and 0 respectively.
There are three basic operators AND, OR and NOT for working with
truth values. These are sometimes referred to as logic gates.
x |
y |
x AND y |
x OR y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
x |
NOT x |
|---|---|
| 0 | 1 |
| 1 | 0 |
Using these axioms more complex logic gates can be built up. For example, by
combining NOT and AND one can create what is commonly referred to as
a NAND gate.
x |
y |
x AND y |
NOT (x AND y) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Importantly one can use Boolean logic gates to implement integer arithmetic and memory. This combined with the fact that it is relatively easy to physically implement Boolean logic using relays led to the construction of the first computers.
Although you may not want to create your own computer, having a basic
understanding of Boolean logic will help you when implementing algorithms. For
example one often needs to make conditional logic statements along the lines of
“IF the cell contains green fluorescent protein AND it is illuminated
with light of wavelength 395 nm THEN it will emit fluorescence at 509 nm”.
Note
Boolean logic is also used in Boolean networks, a formalism that can be used to describe gene regulatory networks at the protein expression level, i.e. mRNA and protein concentrations are not considered. The expression level of each gene is considered to be either on or off, a.k.a. 1 or 0. The state of the model is the set of Boolean values used to describe the gene network transcription levels at that point in time. Inhibition and activation are modeled by creating Boolean rules, which can be further combined using Boolean logic. By iteratively applying the Boolean rules the dynamics of the system can be evaluated over time. As time progresses the number of states of the network decreases as the system is driven towards a relatively small number of dynamic cycles and stable states, known as attractors. The attractors often correspond to specific differentiated states of cells in biological systems.
The microprocessor¶
A microprocessor executes machine instructions. Machine instructions tell the microprocessor what to do. At the most basic level there are three things that a microprocessor can do: perform mathematical operations, move data from one memory location to another, make decisions and jump to new sets of instructions based on those decisions.
Most programming languages provide some sort of abstraction layer so that the programmer does not need to think in terms of machine instructions. For example, the main purpose of a C compiler is to convert C source code into machine instructions.
When working with higher level languages, such as Python, one does not really need to worry about what happens at the microprocessor level.
However, knowing that a microprocessor can make decisions and jump to new sets of instructions can be useful when trying to understand concepts such as loops. A loop is essentially a set of machine instructions that end with a decision to jump back to the beginning of the same set of instructions.
Loops often include a condition for exiting the loop. If the condition for exiting the loop is not defined, or it cannot be reached, the loop will keep cycling forever in what is termed an “infinite loop”.
Below is a basic C program illustrating a while loop. The loop terminates when
the integer i is no longer less than 3.
1 2 3 4 5 6 7 | int main () {
int i = 0;
while( i < 3 ) {
i = i + 1;
}
return 0;
}
|
In more detail, the lines 1 and 7 define a small set of code that forms the
main part of the program. Line 2 defines an integer, i, and sets it equal
to 0. Lines 3 and 5 define a while loop to iterate as long as i is less
than 3. Line 4 executes a command to change the value of i. Line 6 states
that the main program should return an exit status 0.
Computer memory¶
Computer memory comes in different forms with different characteristics. The hard drive of a computer is a type of memory where data can be stored permanently. RAM (Random Access Memory) is a type of memory where data is volatile, i.e. it is not retained when the machine reboots. A less well known type of memory is the registry, which resides in the CPU (Central Processing Unit). Being physically close to the CPU means that reading and writing of data to the registry is very fast. Other important characteristics of computer memory include the its size and cost. Below is a table summarising these characteristics.
| Location | Speed | Size | Cost | Volatile |
|---|---|---|---|---|
| Registry | Very fast | Very small | Very expensive | Yes |
| RAM | Fast | Small/Moderate | Expensive | Yes |
| Hard disk | Slow | Very large | Cheap | No |
One could liken these types of storage to different cooling devices in the lab. The minus 80 freezer is large and represents a way to store DNA plasmids and primers persistently. When preparing for a cloning experiment one may get samples of plasmids and primers and store them in the fridge in the lab for easy access. However, although the lab fridge provides easy access it does not present a permanent storage solution. Finally, when performing the cloning experiment one takes the samples out of the fridge and places them in an ice-bucket. The ice-bucket is a “working storage” solution to which one can have very fast access. In the example above the minus 80 freezer represents the hard disk, the lab fridge represents RAM and the ice bucket represents the registry.
If one is working with really large data sets the main bottleneck in the processing pipeline can be reading data from and writing data to memory. This is known as being I/O (input/output) bound.
Key concepts¶
- A bit is the smallest piece of data that can be stored in a computer, it can be set to either zero or one
- A byte is 8-bits
- An unsigned 8-bit integer can represent any of the integers between 0 and 255
- A character encoding maps characters to integers, common character encodings include ASCII and Unicode
- Real numbers tend to be handled using floating-point representation
- There are some inherent limitations when working with floating-point numbers which can lead to issues with accuracy
- Boolean logic is one of the main tools employed by the computer to do work and to store data
- A microprocessor executes machine instructions
- Machine instructions can tell the microprocessor to perform mathematical operations, move data around and to make decisions to jump to new sets of machine instructions
- The hard disk, RAM and the register are different types of memory with different characteristics
- Processes that spend most of their time reading and writing data are said to be I/O bound